Non-parametric statistics for quantitative traits
This page provides a brief overview of the non-parametric quantitative trait
linkage statistics implemented in MERLIN. These statistics are accessed through
the --qtl and --deviates command line options.
The two non-parametric quantitative trait statistics are implemented in the
general framework of Whittemore and Halpern (1994) and Kong and Cox (1997). The
basic idea in this framework is do define some function S(v) that
allows alternative inheritance vectors for one pedigree to be ranked according
to the evidence for linkage they provide.
Thus, a suitable function should be such that S(v1) >
S(v2)
indicates that inheritance pattern v1
is more suggestive of linkage than v2.
For example, for affected sib pairs, one suitable
definition is S(v)=π(v) where π(v) denotes the number of alleles shared for
inheritance vector v. For discordant sib-pairs, an alternative definition might
be S(v)=-π(v).
For quantitative traits, MERLIN uses the following defintion:
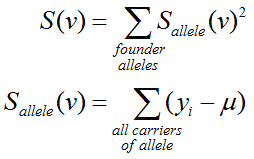
Here, the score for each inheritance vector S(v) is calculated by summing
squared scores for each founder allele. This sum will take larger values when
the scores for individual founder alleles are more extreme. The score for each founder
allele is calculated by simply mean deviates (yi-μ) for all
individuals i who carry the founder allele. Note that yi
is the phenotype for individual i, μ is the population mean and the list of individuals
who carry a particular founder allele is implied by v.
When the --qtl option is selected MERLIN uses the sample mean to estimate μ.
When the --deviates option is selected, MERLIN fixes μ at 0 (zero). The later
option is suitable for the analysis of selected samples if the sample mean is subtracted from
individual phenotypes prior to analysis.
The procedure for converting scores for individual inheritance vectors into Z-scores for
a single or multiple pedigrees is described in detail by Whittemore and Halpern (1994). These
Z-scores are used by MERLIN to construct a likelihood ratio test for linkage and define a LOD score
statistic using the procedure described by Kong and Cox (1997).
MERLIN also implements variance components (--vc option) and regression-based
(MERLIN-REGRESS package) tests of linkage for quantitative traits. Both of these
tests are designed for traits which are normally distributed in the population
and are likely to be more powerful for such traits. Detailed descriptions of
these alternatives are available elsewhere (see for example, Amos, 1994; Sham et al,
2002).
References
Amos (1994) Robust variance-components approach for assessing genetic linkage
in pedigrees. American Journal of Human Genetics 54535-543
Kong and Cox (1997) Allele-sharing models: LOD scores and accurate linkage
tests. American Journal of Human Genetics 61:1179-1188
Sham, Purcell, Cherny and Abecasis (2002) Powerful regression-based quantitative-trait
linkage analysis of general pedigrees. American Journal of Human Genetics
71:238-253
Whittemore and Halpern (1994) A class of tests for linkage using affected
pedigree members. Biometrics 50118-127
| 


