| |
PSEUDO -- Gene dropping method for empirical p-values
One traditional method for evaluating the significance of a lod score score peak obtained from a genome scan
relies on gene-dropping to simulate hundreds or thousands of replicate genomes under the null hypothesis. These
replicates can then be used to reproduce the underlying null distribution for any statistic of interest. For a Kong
and Cox lod score, evaluation of a hypothesis H involves repetition of the following steps several thousand times:
- Simulate pedigree data similar to the original with respect to family relationships, marker placement and
allele frequencies, but assuming no linkage and no association by
gene-dropping
- Perform linkage analysis on the simulated data to generate a lod score profile
(L1,L2 , ... Lp) consisting of one Kong and
Cox lod score for each analysis position.
The algorithm for calculating the ith lod score,
Li is
- Let F = {F1, F2, ... FN } be the set of all families in
the data set. Let G be the set of simulated genotypes.
- For each family Ff in F, calculate a family-specific z-score at position i as
 where where 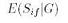 is the expected sharing
score for family f at position i given
genotypes G, and is the expected sharing
score for family f at position i given
genotypes G, and 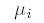 is sharing expected under
the null hypothesis of
no linkage. is sharing expected under
the null hypothesis of
no linkage.
- Calculate the lod score at the ith position as
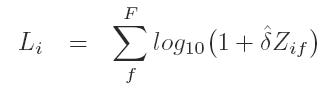 where delta-hat is the maximum likelihood estimate of delta.
where delta-hat is the maximum likelihood estimate of delta.
- Count the simulation as "positive" if the profile of simulated lod scores (L1, L2 ,
... Lp) satisfies H.
For a total of M data sets, estimate a p-value for H as
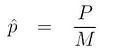 where P is the number of positive simulations.
where P is the number of positive simulations.
References for Kong and Cox tests of linkage
Kong and Cox (1997) Allele-sharing models: LOD scores and accurate linkage tests. American Journal of Human
Genetics 61:1179-1188
Whittemore and Halpern (1994) A class of tests for linkage using affected pedigree members. Biometrics 50118-127
| |



